- Yazar admin [email protected].
- Public 2023-12-17 03:45.
- Son düzenleme 2025-06-01 06:49.
Dönüştürülmüş alan ve yaşam alanı, çok çeşitli konu alanlarında bir binayı tanımlamak için defalarca kullanılan en önemli parametrelerden ikisidir. Yaşam alanı oldukça kolay belirlenebilirken kübik yapı her zaman zorluklara neden olur. Bu neleri içerir ve hesaplamada neler ihmal edilir? Güvenli bir şekilde güvenilir bir sonuca nasıl ulaşabileceğinizi adım adım açıklıyoruz.
Kübik nedir?
" Kübasyon" terimi Latince "cubus" kelimesinden gelir ve doğrudan bir bedeni tanımlar. Ancak binalar söz konusu olduğunda bu gövde, tanımı genişletir ve evin bir bütün olarak kapladığı hacim anlamına gelir. Genel olarak konuşursak, bu, toplam hacmi oluşturan farklı hacimlerin toplamını içerir:
- Net hacim: Kullanılabilir tüm odaların hacmi, binadaki “hava hacmi”
- İnşaat hacmi: Bir binanın tüm bileşenlerinin hacmi, yani duvarlar, tavanlar, çatı vb.
Kübik teknik dilde hala her yerde mevcut olsa da, temel olarak aynı şeyi tanımlayan daha modern bir ifade olan "dönüştürülmüş alan" mevcut düzenlemelerde bulunabilir.
Dönüştürülmüş bir odanın amacı nedir?
Sıradan insanlar her zaman kübik hesaplama konusunda neden bu kadar yaygara çıkarıldığını kendilerine sorarlar. Bu değerin çeşitli kullanımlarına bakıldığında anlamı hemen anlaşılır:
- Maliyet planlama ve izleme
- Bina planlamasına yönelik yasal değerlendirme göstergesi
- İnşaat finansmanı
- Gerçeğe uygun değeri belirlemek için temel
- Bireysel yönler
NOT:
Sözde "bina kütlesi" ni uzman literatürde, içtihatlarda ve düzenlemelerde tekrar tekrar okuyorsunuz. Kurallar dizisine bağlı olarak, karar biraz değişebilir, ancak sonuçta aynı zamanda hacim veya kapalı alanla da ilgilidir.
DIN277-1 hesaplamanın temeli olarak
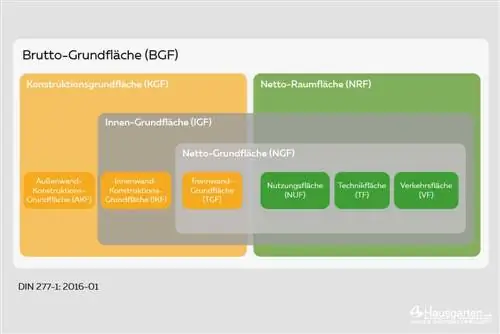
Birkaç eşit derecede önemli belirleme yönteminin mevcut olduğu yaşam veya kullanılabilir alanın belirlenmesinin aksine, kübik hesaplamanın temeli açık ve basittir. Almanya'da kübikliğin belirlenmesine yönelik tüm spesifikasyonları içeren bağlayıcı bir kurallar dizisi bulunmaktadır: DIN 277-1 “İnşaattaki temel alanlar ve hacimler - Bölüm 1: Bina inşaatı”. Bu düzenleme, hacmi belirlemek için ilk kez tek tip bir belirlemenin yapıldığı ve o zamanlar resmi olarak kübik olarak adlandırılan 1934 yılına kadar uzanıyor. Birkaç değişiklik ve revizyondan sonra, bu DIN standardının 2016 tarihli güncel versiyonu bugün geçerlidir.
DİKKAT:
DIN 277-1 bir yasa olmasa da genel olarak uygulanamayan bir standart olsa da artık genel olarak tanınmaktadır ve bu nedenle neredeyse bağlayıcıdır. Teknik bir kural olarak, artık bilinen en ileri teknolojinin bir parçasıdır ve bir anlaşmazlık durumunda mahkemeler tarafından da referans olarak kullanılmaktadır. Kapalı alan farklı hesaplanırsa bu mümkündür, ancak bir anlaşmazlık durumunda denkliğin gerekçelendirilmesi ve kanıtlanması çok büyük çaba gerektirir.
Neler dikkate alınıyor, neler dışarıda bırakılıyor?
DIN'e bir bakış, neyin küplere ait olup neyin olmadığını hemen netleştirir. 7. Bölüm “Bina hacminin belirlenmesi” giriş cümlesi temel içeriği açıkça belirtmektedir:
“Brüt hacimsel içerik (GRI), binanın brüt taban alanının (GFA) üzerinde olan tüm odaların ve bina yapılarının hacmini içerir.”
Ayrıca, kapalı alan veya kübik ile eşanlamlı olan brüt hacmin, bina temellerinin, dış duvarların ve çatı pencereli çatıların dış sınır yüzeyleri tarafından oluşturulduğu da tanımlanmaktadır. Basitçe ifade etmek gerekirse bu, çatı yüzeyinin, dış duvarın dış kenarının ve döşeme levhasının söz konusu hacmin sınırlarını oluşturduğu anlamına gelir. Şimdi bu konunun ayrıntılı olarak nasıl ele alınacağı sorusu haklı olarak ortaya çıkıyor. Bireysel durumlarda bir evde, DIN'in yorumuna bağlı olarak ilave hacim oluşturabilecek veya yaratmayabilecek çok sayıda ayrıntı bulunur. Burada netlik sağlamak adına hangi yapı bileşenlerinin kübik hesaplamaya açıkça dahil edilmediği açıkça düzenlenmiştir:
- Derin ve sığ temeller, yani temeller ve zemin döşemeleri
- Işık direkleri
- Binaya yapısal olarak bağlı değilse harici merdivenler ve rampalar
- Giriş kanopileri
- Çatı çıkıntıları
- Köşeli güneş koruma sistemleri
- Çatı kaplamasının üzerine çıkan bacalar, egzoz ve havalandırma boruları
- Çatı membranının üzerinde maksimum bir metreküp hacme sahip ışık kubbeleri
- Pergolas
- Yer yüzeyinden çıkıntı yapsalar bile güçlü dış mekan oturma yerleri veya teraslar
Özel durum
Bir binanın tamamen kapatılmamış bölümleri hacim hesaplamasında biraz özel bir konuma sahiptir. Bunun örnekleri arasında kapalı duvarları olmayan destekler üzerindeki çatılar yer alır. Ayrıca çatı katları veya balkon korkulukları da yaygındır, yani çatı şeklinde üst “kapak” bulunmayan dikey duvar bölümleri. Burada DIN, sözde hayali bileşenlerin alanı sınırlamak için kullanılabileceğini ve kullanılması gerektiğini açıkça belirtiyor.
Bu ne anlama geliyor?
Bu basitçe çatı katının üst kenarının bu şekilde oluşturulan hacmin üst sınırını temsil ettiği anlamına gelir. Çatı durumunda, hayali dış duvarlar ya desteklerle ya da - desteksiz olarak destekleniyorsa - çatının kenarıyla tanımlanır.
NOT:
Çatı kenarının belirli bir bölümü sıklıkla genişletildiğinden ve dolayısıyla teras çatıyı oluşturduğundan, çatının kenarını ve çatıyı ayırmak o kadar kolay değildir. Burada normalde 0,50 metre limitini kullanabilirsiniz. Çatı çıkıntısı daha büyükse, alan oluşturan bir çatı olarak kabul edilir. 0,50 metreye kadar bu, dikkate alınmayan bir çatı kenarıdır.
Örnek adım adım kullanılarak yapılan hesaplama

Şimdi somut bir örnek kullanarak hacim hesaplamasına bir göz atalım. Hacim belirlememizin amacı olarak aşağıdaki özelliklere sahip tipik bir tek aileli evi ele alıyoruz:
- Uzunluk 10 metre
- Genişlik 8,5 metre
- Saçak yüksekliği (dış duvarın çatı kaplamasıyla kesişme yüksekliği=araziden 3, 50 metre
- sırt yüksekliği 6,00 metre
- Bodrum, zemin döşemesinin üst kenarı yerden 3,00 metre aşağıda
- Çatı şeklinde üçgen çatı
- Çatı çıkıntısı 0, 30 metre
- Ek giriş holü 1, 00 metre genişliğinde, 1, 50 metre derinliğinde, yerden 3,00 metre yüksekliğinde, düz çatı
- Veranda çatı uzantısı, evin kenarından 3,00 metre destek aralığı ve 3,00 metre genişlik, düz çatı, yerden yükseklik 2,50 metre
Adım adım
1. Somut kısmi hacimlere zihinsel ayrıştırma:
- Ev gövdesi, döşeme levhasının saçak yüksekliğine kadar üst kenarı
- Çatı saçak yüksekliğinden sırt yüksekliğine
- ön cam
- Teras çatı
2. Alt yapıların hacim hesabı için matematiksel formüllerin belirlenmesi:
a. Ev Gövdesi: Uzunluk x Genişlik x Yükseklik
b. Çatı: Uzunluk x genişlik x yükseklik x 0,5
c. Rüzgar yakalayıcı: Uzunluk x genişlik x yükseklik
d. Teras çatı: Uzunluk x genişlik x yükseklik
3. Hacmin hesaplanması:
a. Ev gövdesi: 10, 00m x 8, 50m x (3, 50m+3, 00m)=552, 50m³
b. Çatı: 10,00m x 8,50m x (6,00m - 3,50m) x 0,5=212,00m³
c. Rüzgar koruması: 1, 50m x 1, 00m x 3, 00m=4, 50m³
d. Teras çatı: 3,00m x 3,00m x 2,50m=22,50m³
e. Topla a. d'ye.=791, 50m³
Hesaplamayla ilgili notlar
Örnek, kübik hesaplamanın doğru yaklaşımla aslında çok basit olduğunu gösteriyor. Bu ipuçları ve püf noktaları hedefinize hatasız bir şekilde ulaşmanıza yardımcı olacaktır:
Diseksiyon

Hesaplanacak yapıyı, hesaplanması mümkün olduğu kadar kolay olan bireysel hacimlere bölün. Bu, neredeyse her zaman okul günlerinizden bildiğiniz küboid veya üçgen cisim formüllerini kullanabileceğiniz anlamına gelir.
Çatı eğimi
Çatı ne kadar dik olursa olsun ve ister simetrik ister asimetrik olsun, eğimli çatılar her zaman uzunluk x genişlik x yükseklik x 0,5 formülü kullanılarak hesaplanabilir. Eğer bunu 90 derece eğimli çatı yüzeyine sahip beşik çatının özel bir şekli olarak anlarsanız, tek eğimli çatılar bile bu şekilde hesaplanabilir.
Özel bileşenler için alt kenar
İster giriş holü ister teras çatı olsun, yapısal bir alt kenar olmadığında arazi yüzeyi hacmin alt sınırı olarak görülebilir. Örneğin, giriş kapısı eğimli bir arazide bulunuyorsa ilgili yükseklik olarak giriş kapısındaki arazinin yüksekliğini kullanın.






